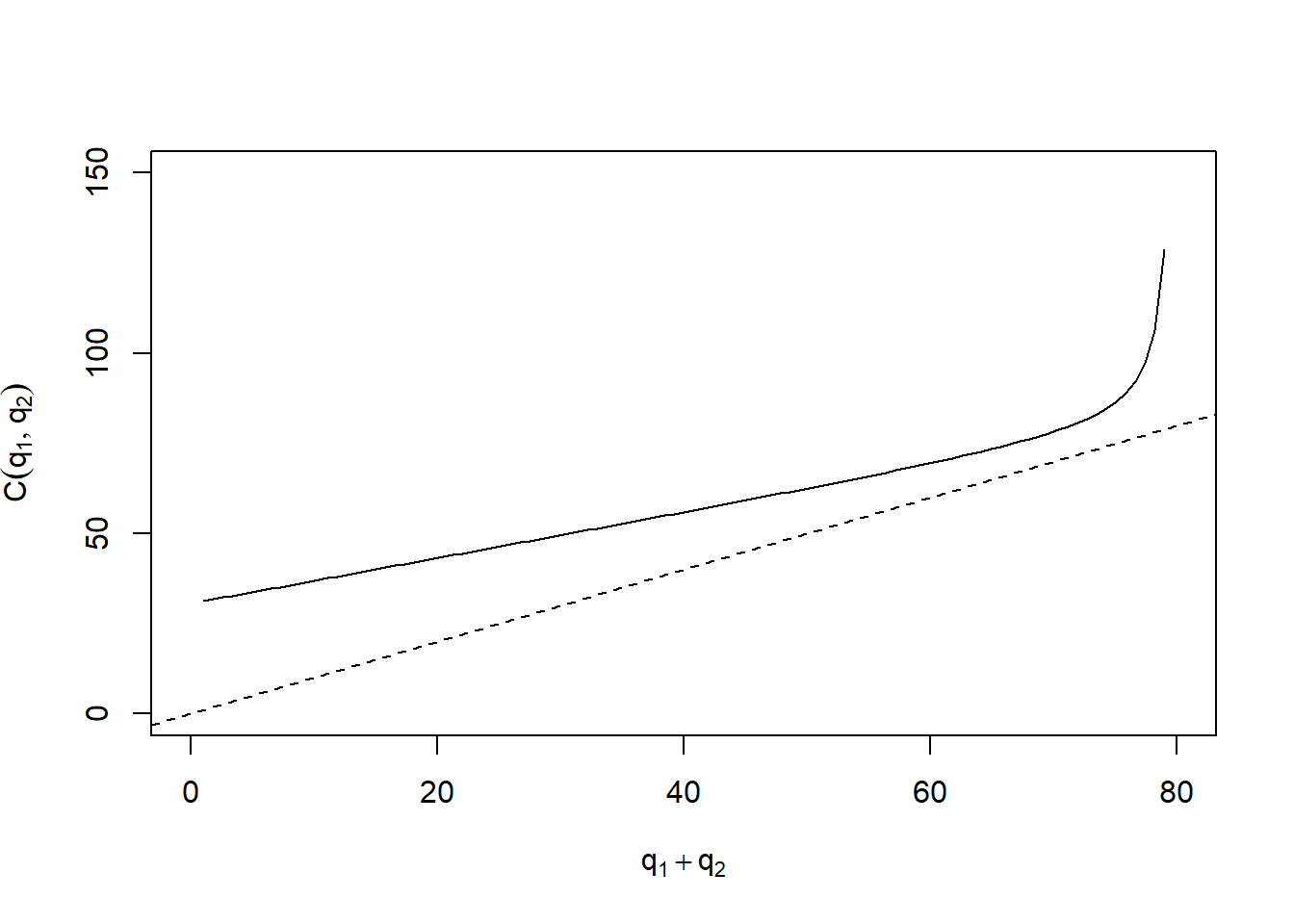
Drastically reducing net immigration has been a stated policy aim of the UK government for over a decade, and visas relating to international students (study visas and post-study work visas) have been in their sights more recently.
On one side of the argument, it is claimed that international students have places at UK universities at the expense of domestic students. Parents are upset that their children are losing out to international students, especially when there is the suggestion that entry requirements are lower.
On the other side of the argument, it is only thanks to international students that universities are solvent and able to provide places to any domestic students. It is claimed that the cost of providing a typical course is less than the fees paid by domestic students (£9,250), and therefore domestic students are directly subsidised by international students and reductions in international students will only result in fewer places for domestic students.
There are two nuances missing from this discussion:
- There is a critical difference between average and marginal costs;
- There is heterogeneity between and within universities.
A simple economic model can show that both sides are partially correct.
Average and marginal costs
The average cost of providing a course is simply the total cost of providing the course divided by the number of students.
If we let \(q_1\) and \(q_2\) be the number of domestic and international students respectively on a course, then the cost of providing the course can be a function \(C(q_1, q_2)\).
The average cost is then
\[ AC(q_1, q_2) = \frac{C(q_1, q_2)}{q_1+q_2} \]
Marginal costs are the additional cost associated with additional students on the course, which are
\[ \begin{aligned} {MC}_1(q_1, q_2) &= \frac{\partial C(q_1, q_2)}{\partial q_1} \\ {MC}_2(q_1, q_2) &= \frac{\partial C(q_1, q_2)}{\partial q_2} \end{aligned} \]
Universities will make their decisions based on marginal costs and marginal revenues – while each new student increases revenue more than it increases costs (marginal revenue is greater than marginal cost, \(MR > MC\)), universities will continue to grow.
The decision of whether to grow, shrink, or maintain the current size is not based on average costs (or average revenue). But if average costs exceed average revenue then the course is loss-making and will likely be shut down.
Running a course incurs a substantial amount of fixed costs, but variable costs may not be all that high.
For the sake of argument, we can imagine a cost function as shown below:
We have set the unit of costs to be 1× the cap on domestic student fees, so that the dashed line shows the revenue if all students pay the domestic student fees. With this cost function, the average cost exceeds the fees received per domestic student, so the course must recruit some international students or go bust.
The actual cost function is
\[ C(q_1, q_2) = c_0 + c_1 q_1 + c_2 q_2 + \frac{c_3}{q_{max} - (q_1 + q_2)} \]
with \(c_0 = 30\), \(c_1 = 0.6\), \(c_2 = 0.8\), \(c_3 = 50\) and \(q_{max} = 80\). In the figure above, we have \(q_1 \gg q_2\).
This cost function includes significant fixed costs and a ceiling on the total number of students who can be educated.
Now consider the demand for places on the course. For a typical course, there is always excess demand from domestic students, i.e., \(q_1\) can be set to any number without needing to lower the price for domestic students below 1× the domestic fees cap.
Demand from international students will be more elastic, so that if the price is increased, demand will fall. For simplicity we can assume that the price elasticity of demand is constant:
\[ D_2 (p_2) = d_1 p_2^{\varepsilon_2} = 40 p_2 ^ {-1.5} \]
So if the fees for international students are equal to the cap on fees for domestic students (\(p_2 = 1\)) there will be demand for 40 places from international students, and for every 2% increase in the price, the demand will drop by 3%.
The final step is to include a model for how the university will set \(q_1\) and \(p_2\) (the number of domestic students to admit and the price for international students). It will set these jointly to maximise profits, which are given by
\[ \pi(q_1, p_2) = q_1 + D_2 (p_2) p_2 - C(q_1, D_2 (p_2)) \]
Given these functions, profit is maximised by taking 63 domestic students and setting international fees to 3.542 (£32,765 per year) such that 6 international students are enrolled. The resulting profit is 7.107 (£65,746 per year).
What happens now if through government policy, the course is less attractive to international students?
Suppose that this results in \(d_1 \rightarrow 20\), i.e., for any given price, the number of international students who will apply is halved versus before.
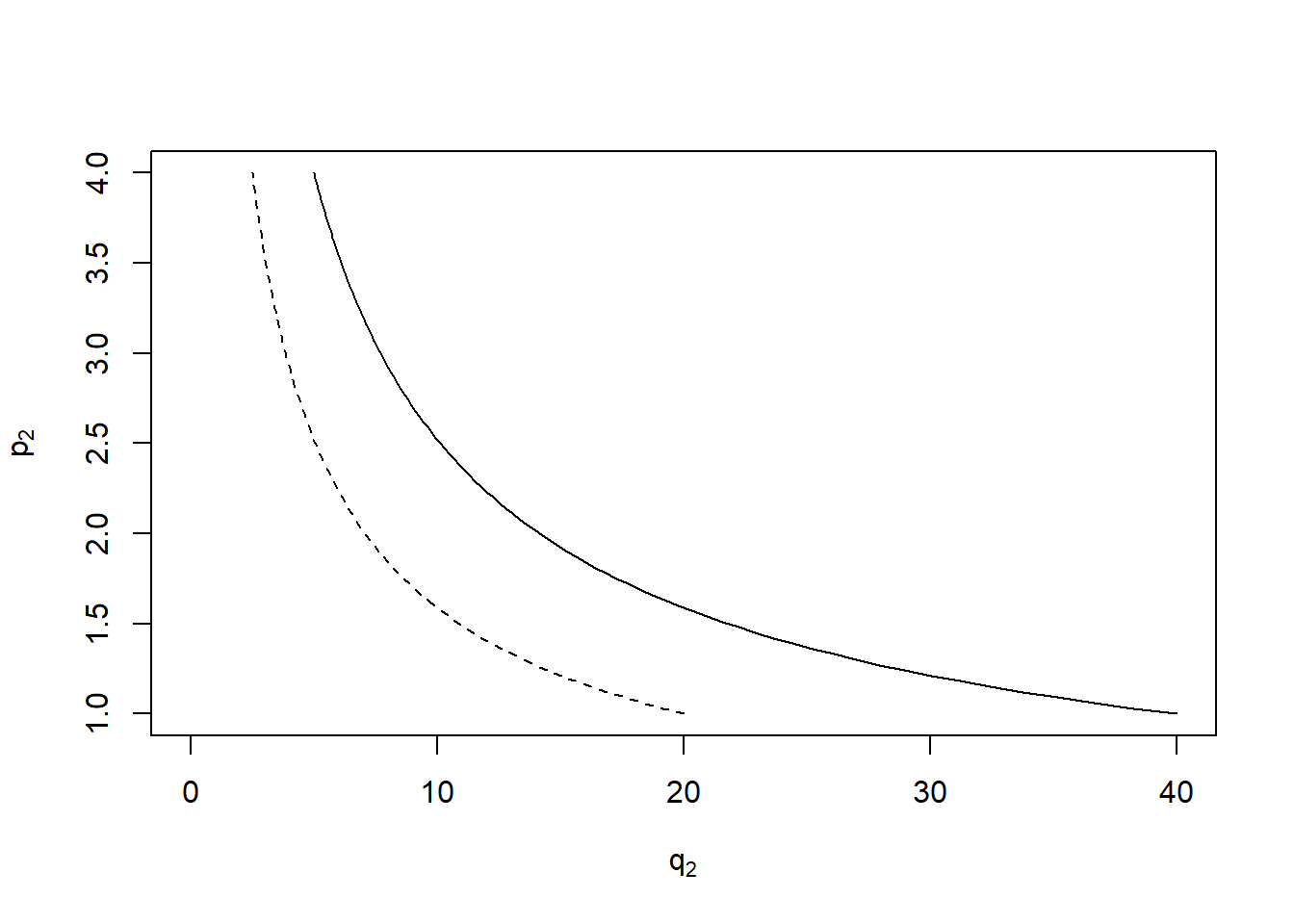
Well now profit is maximised by taking 66 domestic students and 3 international students (the optimal price doesn’t change, but the shift in demand means fewer international students). Profit is slashed to 0.081 (£750 per year).
Let’s reflect on what has happened.
The government took action to make the UK higher education sector less attractive to international students. When it did this, demand for places fell and the number of places given to domestic students increased 1:1.
In a sense this is a policy success; the government wanted to reduce immigration (it did) and it wanted to increase the places for domestic students (it did).
But note the (possibly unintended) consequence – the course is now barely financially sustainable. Without some form of compensation, any further shock on international student demand could lead to the course closing.
Heterogeneity between and within universities
Not all universities are the same, and not all courses within a university are the same.
There will be different cost functions, e.g., courses which rely mostly on lectures instead of one-to-one or small group work can scale more cheaply.
There will be different demand functions for international students – a prestigious programme can attract many more students for the same price than a programme without the prestige. For some courses there may also be limitations on the number of domestic students who can be attracted.
There may also be behavioural factors which mean universities don’t necessarily go all out to maximise profits. They may not want the fees they charge to international students to be significantly out of line with fees charged by “benchmark” institutions. They may not want international students to exceed a certain proportion of the overall cohort.
But what is important is this: not all university courses will survive a policy-driven tightening of international student demand. This could lead to an overall reduction in domestic student places rather than an increase.
Conclusions
As I said, both sides are partially correct. It is entirely plausible that if policy successfully reduced international demand (e.g., by restricting post-study work visas), the number of places for domestic students would increase to fill the gap. But given the allegedly tight financial situation for universities, it is also possible that the consequence would be a loss of courses and therefore a reduction in places overall.
Unless the government is willing to compensate universities for lost demand from international students, or to increase the income per domestic student1 (both of which seem unlikely), some courses (and maybe some whole institutions) will go under.
Perhaps this is a not-unintended consequence of marketisation. Certainly it is clear the government believes some courses (with poor subsequent earnings for graduates) should close. Many have speculated that there is even an unspoken policy aim that some institutions should be allowed to fail and be removed from the market.
At the end of the day, whether restricting international students will lead to more or fewer places available for domestic students depends on the current financial health of universities and how that varies between and within institutions. It is not possible to say that decreasing international students with certainty decreases or increases places for domestic students. We can only hope, since neither the Conservatives nor Labour are committing to improving the financial arrangements for universities, that an incoming Labour government will at least ease off attempting to reduce immigration by specifically targeting students.
Footnotes
Note that the increase in income doesn’t need to come from increased fees if the government was prepared to subsidise.↩︎